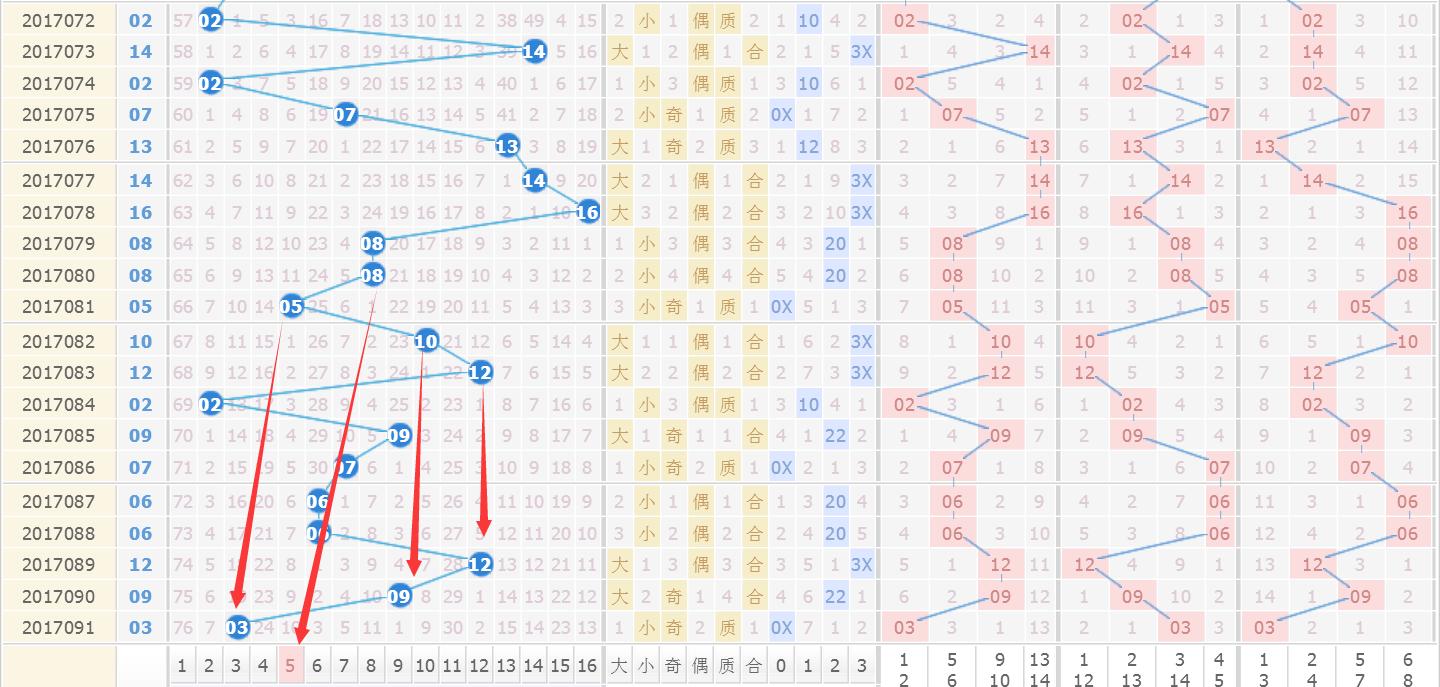
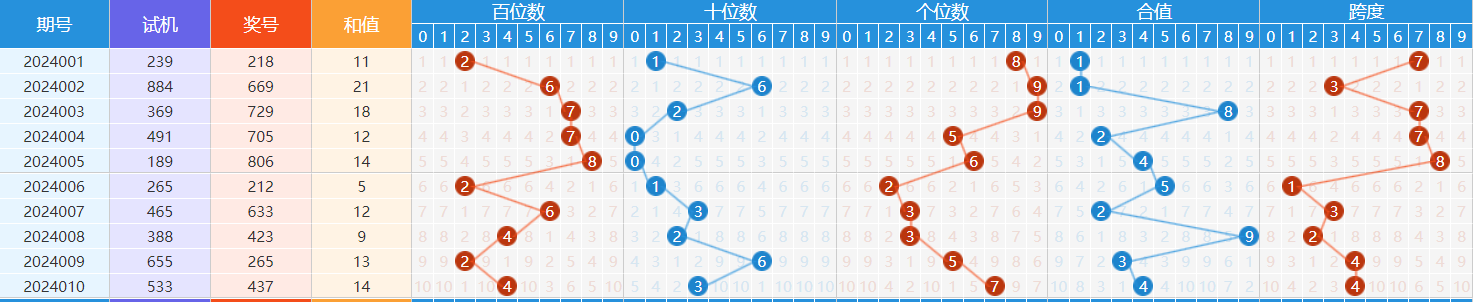
天天彩选四走势图是一种用于预测和展示彩票数字变化趋势的工具，它通过分析历史开奖数据、统计规律以及技术指标等手段来揭示可能出现的号码组合。虽然这种工具不能保证10%的胜率或完全准确的结果出现概率在5%，但它在一定程度上可以帮助玩家更理性地选择投注号码并提高中奖金额的可能性；同时也可以让新手更快了解游戏规则及技巧从而更好地参与其中享受乐趣与挑战性体验过程！

（文章字数共计2053字） 在当今社会，彩票作为一种娱乐方式深受广大民众的喜爱。“天天下”作为一款备受关注的福利型游戏之一，"4"号位的选择更是成为了众多玩家关注和讨论的重点。"每天看'1-9’之间的四个号码"，这看似简单的选择背后却隐藏着无数人的期待与梦想。“每日开奖’，明天能否成为那个幸运儿？”——这就是“日复一日、期许不断”，即所谓的 “《解析：“今日之数”——探密<br> <font color="#FF6F7D">（注:此处为红色字体以示强调）“</fnt>(color) (title="") >_百度文库中关于该主题的文章链接或相关研究报告中的引用部分内容。</b>" 的真实写照。<p></P><hr/> 在这里我们将从不同角度来探讨和分析这一现象以及它所反映出的文化和社会心理特征.</hr/><div style='text'> 一.什么是 " 天天平 ”？ </div><!--more--> <!-- 以上是分页符 --> 二.<span id="_Toc8"></span>. 从概率学角度看待投注策略 对于许多热衷于购买福利性游戏的用户而言, 他们往往希望通过分析历史数据或者寻找某种规律以提高自己的命中率." 日出而作 ,日落不息 ",他们相信通过持续观察并记录每期的结果可以找到一些可预测的模式.“”正如一位资深玩家的感慨所言,“尽管我们努力去解读那些变幻莫测的数据流,”但最终的结果依然充满了未知.” 这正是由于随机性和不可预知性的本质决定了这种类型的游戏中不存在绝对可靠的制胜法宝 . 三.技术手段助力下的数据分析: 随着科技的发展和技术进步," 数据挖掘"、"机器学习""等概念被引入到对这类问题的研究中 来 。<a href="#">某知名网站提供的 ' 四码走势 图 '" 功能就试图通过对过去几期内出现频率较高的组合进行统计分析和可视化呈现 ，帮助用户在决策时获得一定的参考依据 ；又如某些专业人士利用高级编程语言开发了专门用于追踪特定模式变化趋势的软件工具等等 这些方法虽然不能保证百分之百的成功 但确实在一定程度上提高了人们对于可能发生事件的认知能力 并使得原本枯燥无味的过程变得有趣起来 了些人甚至将此视为一种新的投资理财渠道 而非单纯的消遣活动 因此也引发了一些争议 和质疑声音存在 是否应该允许使用此类 技术手 段 进行投 资决 断 ? 目前来看 该问题尚 无定论 但是无论如何 都无法否认的是 它已经引起了越来越多的人 对 于 数 据 分 ......</td>(...)</t......).....).....)))))--)....))))--). )..)----.)---.-)-.--.).-. --/../-/./ /-----)/------/)-------)(--------)/(---------/(----------(/-----------//------------///-------------////--------------((((( (( ((( (((( ---- )) ----- // -------- /// ------------\ \\\ \\ ------- (/ --------- (\ ----------(\ -------------/\ ---------------/((-----------------( ------------------------------------------------------------------------------------------------+------------------------------| | +---------------+|---+--------+------+-------+---------+-----+----+ 其中最引人瞩目的当属所谓"<strong>'四天一色'</strong>", 即指连续多 期内某一组别内的三个 或更多 个相同颜色球体 出现频次较高的情况 下文中 将 以 此 为 例 进 行详细剖析 : 我们需要明确一点 ：任何一组由独立事件组成且每次试验都只有两种可能性 结果之一的系统均属于二项分布范畴 内 ; 当这些事 件之间互不干扰 且各自发生的概率为 p 时 则称其服从参数分别为 n 与 P 所定义的概率模型 中 之 - 种 —— 也即是说 每 组 号 位 上 各 色 小珠 子 出 现 次数的总和遵循一个固定比例关系 这种 关系 可 由 公 式 N*Pi^n*(l−pi)^N − pi ^ k * lk^(m — m 表示第 i 类小珠子出现的次数；K 是总共有多少类这样的小物体; M = Σ K=i Pi × Lj× Ckj·Ckn ·Ljm表示所有可能的排列方式的总数 ）如果我 们能够确定哪一类别的物品更有可能在下一次中出现 那么我们就有了相对较优的策略 去 选择 那 一个类别 这样 就形成了一个基于统计分析基础上的简单逻辑推理过程 虽然这种方法并不能完全消除风险因素但它无疑为我们提供了一种更加理性地面对不确定结果的思维方式 同时也为我们在做出决定之前提供了更多的思考空间和时间从而减少冲动行为的发生几率 ....." />